Rプログラミングの小ネタ

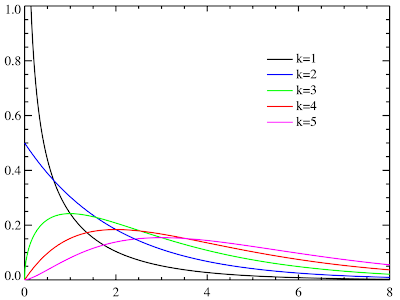
カイ二乗分布といえば、独立性の検定や適合度の検定で使ったりしますよね。 ウィキペディア には、確率密度関数のグラフが載っていて↓こんな感じ。 カイ二乗分布の確率密度関数のグラフ このグラフをRで描いてみようと、確率密度関数の式を見てみると、 ↑こんなのが載っていて、なんだかすごくむつかしい。Γ（ガンマ）関数ってのが出てきて、さらにそれは積分の形で定義されていたりして。 でもまあ、そのへんは理解できなくても、Rにはカイ二乗分布の確率密度関数（dchisq）が用意されているので、下記のようにすれば、ウィキペディアに載っていたのとそっくりのグラフが描けます。 curve ( dchisq ( x , 1 ) , xlim= c ( 0 , 8 ) , ylim= c ( 0 , 1 ) , col = "black" , ylab= "dchisq(x, k)" ) curve ( dchisq ( x , 2 ) , xlim= c ( 0 , 8 ) , ylim= c ( 0 , 1 ) , col = "blue" , add=T ) curve ( dchisq ( x , 3 ) , xlim= c ( 0 , 8 ) , ylim= c ( 0 , 1 ) , col = "green" , add=T ) curve ( dchisq ( x , 4 ) , xlim= c ( 0 , 8 ) , ylim= c ( 0 , 1 ) , col = "red" , add=T ) curve ( dchisq ( x , 5 ) , xlim= c ( 0 , 8 ) , ylim= c ( 0 , 1 ) , col = "magenta" , add=T )   #凡例 legend ( "topright" , lty= 1 , legend = c ( "k=1" , "k=2" , "k=3" , ...

データを公開するときはCSV形式みたいに、RAWデータかそれに近い形で提供してくれると、いろいろと利用できて嬉しいですよね。 原子力規制委員会のサイト では、モニタリングポストで測定された空間線量のデータをCSV形式で公開しているので、これを使って時系列データの可視化を試してみましょう。 下記のページで、都道府県やエリア、期間の日付を選択してダウンロードできます。 ダウンロード | 東日本大震災関連情報 放射線モニタリング測定結果等 | 原子力規制委員会 試しに東京都の都健康安全研究センターのモニタリングポストのデータを2014年1月1日～2014年12月31日の1年分ダウンロードしてみました。10分ごとのデータなのでかなりの量ですね。約5.5MBくらいありました。 まずは、読み込んで、冒頭部分を表示。 > d <- read.csv ( "新宿2014.csv" , header=F , as.is=T ) > head ( d ) V1 V2 V3 V4 1 東京都全域 新宿区　都健康安全研究センター 35.70608 139.6987 2 東京都全域 新宿区　都健康安全研究センター 35.70608 139.6987 3 東京都全域 新宿区　都健康安全研究センター 35.70608 139.6987 4 東京都全域 新宿区　都健康安全研究センター 35.70608 139.6987 5 東京都全域 新宿区　都健康安全研究センター 35.70608 139.6987 6 東京都全域 新宿区　都健康安全研究センター 35.70608 139.6987 V5 V6 V7 V8 V9 V10 V11 1 2014 / 12 / 31 23 : 50 0.034 μSv/h 0.061 μSv/h ‐ NA 2 2014 / 12 / 31 23 : 40 0.033 μSv/h 0.059 μSv/h ‐ NA 3 2014 / 12 / 31 23 : 30 0....

Rには移動平均そのものずばりを求める関数はないようです。でも、filter関数を使えば簡単に実現できます。 まずは、filter関数の動きを確認。 xを時系列データとします。 > x <- c(1, 2, 3, 1, 2, 9, 4, 2, 6, 1) > x  [1] 1 2 3 1 2 9 4 2 6 1 このxにfilter関数を適用すると、 > filter(x, c(1,1,1)) Time Series: Start = 1 End = 10 Frequency = 1  [1] NA  6  6  6 12 15 15 12  9 NA となります。 c(1,1,1)の3つの要素は、（時点 n-1，現時点 n，時点 n+1）に対応します。重みに差を付けられるのですが、ここでは同等にしたいので、すべて1にしています。端の要素は前後の要素がないのでNAとなります。 ↓こんな感じですね。 Rのfilter関数の適用イメージ これだけだと、（時点 n-1，現時点 n，時点 n+1）を足したものになってしまうので、足した要素の数（上記だと3）で割れば、移動平均を取ることになりますね。 ということで、ごくシンプルな移動平均は↓こんな感じで実現できます。 filter(x, c(1,1,1)) / 3 平均を取る幅を広げて、n-2, n-1, n, n+1, n+2 のように5つ分にしたい場合は、 filter(x, c(1,1,1,1,1)) / 5 とやればOK。 分かりやすいように c(1,1,1)、c(1,1,1,1,1))とベタに書きましたが、数が増えた場合も考えて rep(1,3)、rep(1,5)のように書くのが普通ですかね。 何度も使うなら、 moving_average <- function(x, n){   filter(x, rep(1,n)) / n } のように関数化してしまってもいいかもしれません。 【蛇足】 最初「filter」っていう関数名がピンとこなかったんですが、画像処理で使うフィルタと同じ概念なんだと気付いて納得しました。ある...