Rの様々な種類のグラフでデータの分布を理解する(hist、boxplot、stripchart)
データがどんな感じで分布しているか見たいとき、とりあえず視覚化してみますよね。Rだと簡単だし。
で、どんな視覚化があるかというと、ヒストグラム(度数分布図)はお馴染みですが、その他にも、箱ひげ図や一次元散布図なんかがあります。
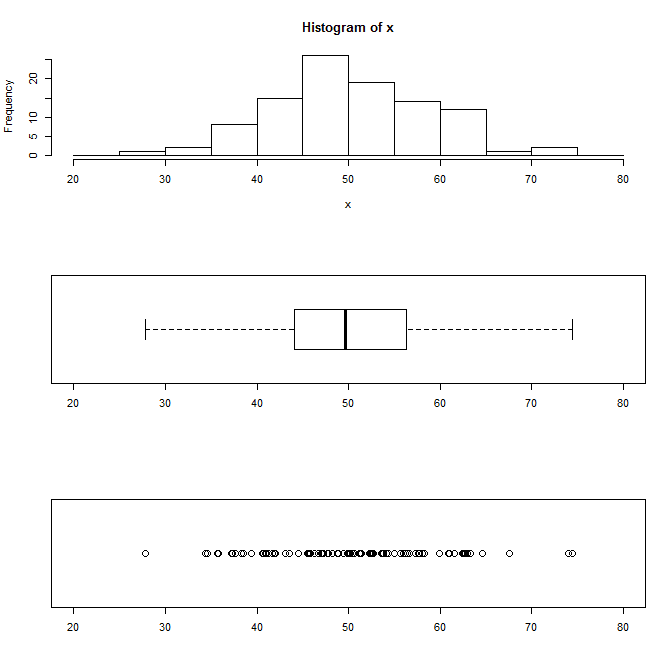
下記は、正規分布に従う100個のランダムデータを発生させ、同じデータをそれぞれのやり方で視覚化したものです。
ヒストグラムは学校でも習ったし、直感的にも分かりやすいですよね。度数が高さで表されているので、量的にも理解しやすい。
箱ひげ図の意味は、以下のようになっています。
ひげの左端 ・・・ 最小値
箱の左端 ・・・ 25%点
中央の太線 ・・・ 中央値(50%点)
箱の右端 ・・・ 75%点
ひげの左端 ・・・ 最大値
慣れないとピンとこないかもしれません。
一次元散布図は、データをそのまま座標にプロットした感じですね。データ数が多くなってくると、データの粗密はなんとなく分かりますが、数はよく分からなくなってしまいます。
こうやって並べてみると、ヒストグラムでいいじゃんって気もしますが、そうでない場合もあります。複数のデータを比較したいような場合は下の2つの方が使いやすい気がします。
↓こんな感じで、標準偏差の異なる複数のデータを作ってみます。
> sd_05 <- rnorm(100,50, 5)
> sd_10 <- rnorm(100,50,10)
> sd_15 <- rnorm(100,50,15)
> sd_20 <- rnorm(100,50,20)
> sd_25 <- rnorm(100,50,25)
> sd_30 <- rnorm(100,50,30)
>
> x <- data.frame(sd_05,sd_10,sd_15,sd_20,sd_25,sd_30)
>
> head(x)
sd_05 sd_10 sd_15 sd_20 sd_25 sd_30
1 46.86773 43.79633 56.14103 67.87347 76.86102 52.31909
2 50.91822 50.42116 75.33310 29.05404 97.39137 41.09394
3 45.82186 40.89078 73.79883 89.42675 34.92507 14.50273
4 57.97640 51.58029 45.03638 42.32736 40.22830 50.33878
5 51.64754 43.45415 15.72147 83.08291 39.59445 79.74803
6 45.89766 67.67287 87.46492 80.24425 40.60856 97.81902
複数のグラフを並べてみます。
↓ヒストグラム
無理矢理に縦に並べてみましたが、やっぱり場所をとりますね。
↓下記みたいに、2列にすればレイアウト的にはすっきりしますが、比較しにくくなります。
箱ひげ図だと、↓こんな感じになります。
箱ひげ図のデフォルトは縦方向なので、「水平だぞ」というhorizontalオプションを付けています。
一次元散布図だと、↓こんな感じになります。
プロットする記号は□(pch=0 デフォルト)よりは、○(pch=1)の方が見やすいかなと思います。
箱ひげ図も一次元散布図も、基本的には一次元的な表現方法なので場所をとりませんね。
以下は30個並べてみたものですが、なんとか見られますね。
↓一次元散布図
一次元散布図は密度が高いと、プロットがつぶれちゃうので、データ数が少ないとき向きのように思います。被験者が10人とか。↓こんな感じ。
これくらいのデータ数だと、個々のデータの値が見える一次元散布図のメリットが出てきますね。
で、どんな視覚化があるかというと、ヒストグラム(度数分布図)はお馴染みですが、その他にも、箱ひげ図や一次元散布図なんかがあります。
下記は、正規分布に従う100個のランダムデータを発生させ、同じデータをそれぞれのやり方で視覚化したものです。
ヒストグラムは学校でも習ったし、直感的にも分かりやすいですよね。度数が高さで表されているので、量的にも理解しやすい。
箱ひげ図の意味は、以下のようになっています。
ひげの左端 ・・・ 最小値
箱の左端 ・・・ 25%点
中央の太線 ・・・ 中央値(50%点)
箱の右端 ・・・ 75%点
ひげの左端 ・・・ 最大値
慣れないとピンとこないかもしれません。
一次元散布図は、データをそのまま座標にプロットした感じですね。データ数が多くなってくると、データの粗密はなんとなく分かりますが、数はよく分からなくなってしまいます。
こうやって並べてみると、ヒストグラムでいいじゃんって気もしますが、そうでない場合もあります。複数のデータを比較したいような場合は下の2つの方が使いやすい気がします。
↓こんな感じで、標準偏差の異なる複数のデータを作ってみます。
> sd_05 <- rnorm(100,50, 5)
> sd_10 <- rnorm(100,50,10)
> sd_15 <- rnorm(100,50,15)
> sd_20 <- rnorm(100,50,20)
> sd_25 <- rnorm(100,50,25)
> sd_30 <- rnorm(100,50,30)
>
> x <- data.frame(sd_05,sd_10,sd_15,sd_20,sd_25,sd_30)
>
> head(x)
sd_05 sd_10 sd_15 sd_20 sd_25 sd_30
1 46.86773 43.79633 56.14103 67.87347 76.86102 52.31909
2 50.91822 50.42116 75.33310 29.05404 97.39137 41.09394
3 45.82186 40.89078 73.79883 89.42675 34.92507 14.50273
4 57.97640 51.58029 45.03638 42.32736 40.22830 50.33878
5 51.64754 43.45415 15.72147 83.08291 39.59445 79.74803
6 45.89766 67.67287 87.46492 80.24425 40.60856 97.81902
複数のグラフを並べてみます。
↓ヒストグラム
無理矢理に縦に並べてみましたが、やっぱり場所をとりますね。
↓下記みたいに、2列にすればレイアウト的にはすっきりしますが、比較しにくくなります。
箱ひげ図だと、↓こんな感じになります。
boxplot(x,horizontal=T)
箱ひげ図のデフォルトは縦方向なので、「水平だぞ」というhorizontalオプションを付けています。
一次元散布図だと、↓こんな感じになります。
stripchart(x,pch=1)
プロットする記号は□(pch=0 デフォルト)よりは、○(pch=1)の方が見やすいかなと思います。
箱ひげ図も一次元散布図も、基本的には一次元的な表現方法なので場所をとりませんね。
以下は30個並べてみたものですが、なんとか見られますね。
↓一次元散布図
n <- 30 x <- data.frame(matrix(rep(0,n*100),ncol=n)) for(i in 1:n){ x[,i] <- rnorm(100,50,i) } stripchart(x,pch=1)
一次元散布図は密度が高いと、プロットがつぶれちゃうので、データ数が少ないとき向きのように思います。被験者が10人とか。↓こんな感じ。
これくらいのデータ数だと、個々のデータの値が見える一次元散布図のメリットが出てきますね。









コメント
コメントを投稿