Rでカイ二乗分布の確率密度関数のグラフをシミュレーション的に描く

カイ二乗分布といえば、独立性の検定や適合度の検定で使ったりしますよね。

ウィキペディアには、確率密度関数のグラフが載っていて↓こんな感じ。

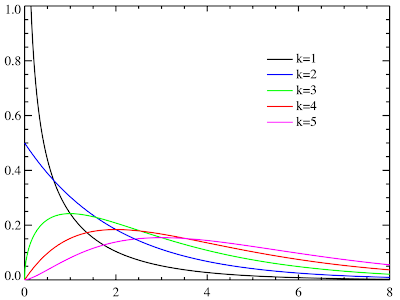カイ二乗分布の確率密度関数のグラフ

このグラフをRで描いてみようと、確率密度関数の式を見てみると、



↑こんなのが載っていて、なんだかすごくむつかしい。Γ（ガンマ）関数ってのが出てきて、さらにそれは積分の形で定義されていたりして。

でもまあ、そのへんは理解できなくても、Rにはカイ二乗分布の確率密度関数（dchisq）が用意されているので、下記のようにすれば、ウィキペディアに載っていたのとそっくりのグラフが描けます。

curve(dchisq(x,1), xlim=c(0,8), ylim=c(0,1), col="black", ylab="dchisq(x, k)")
curve(dchisq(x,2), xlim=c(0,8), ylim=c(0,1), col="blue"   , add=T)
curve(dchisq(x,3), xlim=c(0,8), ylim=c(0,1), col="green"  , add=T)
curve(dchisq(x,4), xlim=c(0,8), ylim=c(0,1), col="red"    , add=T)
curve(dchisq(x,5), xlim=c(0,8), ylim=c(0,1), col="magenta", add=T)
 
#凡例
legend( "topright", lty=1,
        legend = c("k=1"  , "k=2" , "k=3"  , "k=4", "k=5"),
        col    = c("black", "blue", "green", "red", "magenta") )

Rのdchisqを使って描いたカイ二乗分布の確率密度関数のグラフ

で、ここから先は、関数が用意されているにもかかわらず、シミュレーション的なやり方を用いてわざわざ自力で、カイ二乗分布の密度関数曲線を描いてみるという、まったく実用性のない話です。でも、実感みたいなものは湧くかも。

カイ二乗分布の定義はシンプルで、ウィキペディアによると、

独立に標準正規分布に従う k 個の確率変数 X1, ..., Xk をとる。 このとき、統計量

の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。

となっています。

正規分布に従う変数を二乗していくつか足せばいいのか、意外と簡単。

試しに、乱数を発生させて描いてみよう。

n <- 1000000
Z <- (rnorm(n))^2 + (rnorm(n))^2 + (rnorm(n))^2
hist(Z, breaks=seq(0, max(Z)+1, 0.2), freq=F, ylim=c(0,1))

3つ足したんで、k=3の緑の線に対応します。形を見てみると意図通りになってるっぽいですね。

複数のヒストグラムだと重ねたときに見づらいので、カーネル密度推定（density関数）を使って曲線で描画してみましょう。

n <- 1000000
 
X1 <- rnorm(n)
X2 <- rnorm(n)
X3 <- rnorm(n)
X4 <- rnorm(n)
X5 <- rnorm(n)
 
Z1 <- X1^2
Z2 <- X1^2 + X2^2
Z3 <- X1^2 + X2^2 + X3^2
Z4 <- X1^2 + X2^2 + X3^2 + X4^2
Z5 <- X1^2 + X2^2 + X3^2 + X4^2 + X5^2
 
plot(0, 0, type="n", xlim=c(0,8), ylim=c(0,1), xlab="", ylab="")
lines(density(Z1), col="black")
lines(density(Z2), col="blue")
lines(density(Z3), col="green")
lines(density(Z4), col="red")
lines(density(Z5), col="magenta")

k=1、k=2のゼロに近いところでは、かなりずれが大きいですが、それ以外ではけっこう近い曲線になったんじゃないでしょうか。