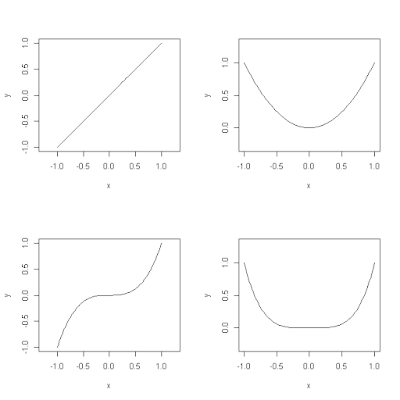
Rのhistとggplot(geom_histogram)を比較する

ggplot2パッケージって使ったことありませんでした。記法がとっつきにくいというのもあったのですが、あの見た目を素直に「きれい」とは認めたくなかったというか。「ggplotの方がかっこいい」という人への反発みたいな部分も多分にあるのですが。 「白地に線画」みたいなビジュアルが好きなんです。下手に色をつけたらかえって趣味が悪くなったりするじゃないですか。自分自身センスがないことを自覚しているので、色やら塗りつぶしやら飾りっぽいものやらは極力使わないようにしていたんですよね。 でも今回、ggplot2パッケージを使ってみようと思ったのは、ベースとなるレイヤーを用意して、次に重ねたいレイヤーを(場合によっては複数)用意して、最後にバンっとplotする、っていうコンセプトがなんだか使いやすいのではないかという気がしたから。なので、徐々に試していこうかなと思っています。 前置きが長くなりました。 今回はヒストグラムですが、多くの人に馴染みのあるデフォルトのhistでの描画と、ggplot2パッケージを使った場合とで、どんな風に違うのか試してみました。 正規分布に従う乱数を発生させて、普通にヒストグラムを描いてみます。 data1 <- rnorm ( 1000 ) hist ( data1 ) 通常のhist関数で描画 ggplot2パッケージを使うと↓こんな描き方になります。 install.packages ( "ggplot2" ) library ( ggplot2 ) df1 <- data.frame ( data1 ) # データフレームにしておく必要がある g <- ggplot ( df1 , aes ( x=data1 ) ) # 対象がdata1列であることを指定 g <- g + geom_histogram ( ) # ヒストグラムを描画することを指定 plot ( g ) # 描画 ggplot2パッケージを使ったもの 先ほどの、デフォルトのhistと階級幅を合わせる(=0.5)には、binwidthを指定します↓ g ...