ベンフォードの法則をRでシミュレーションする
電気料金の請求書の金額の1桁目をたくさん集めて、その分布を見たらどうなっているでしょう。
数字の出方に法則性があるようにも思えないから、1から9まで一様になっているのでは? という気もしますが、そうではないというのがベンフォードの法則です。
ベンフォードの法則 - Wikipedia
ベンフォードの法則は、自然界に出てくる多くの(全てのではない)数値の最初の桁の分布が一様ではない、ある特定のものになっているというものである。
(中略)
この直感に反するような結果は、電気料金の請求書、住所の番地、株価、人口の数値、死亡率、川の長さ、物理・数学定数、冪乗則で表現されるような過程(自然界ではとても一般的なものである)など、様々な種類の数値の集合に適用できることがわかっている。
どのように偏って分布しているかというと、↓こんな割合になるとのこと。
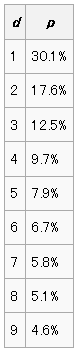
ベンフォードの法則 - Wikipedia より
本当にそうなるか、Rでシミュレーションしてみましょう。
数値が満たすべき分布について、ウィキペディアには、
論理的には、数値が対数的に分布しているときは常に最初の桁の数値がこのような分布で出現する。
とあります。いまいちピンとこなかったのですが、あわせて掲載されていた図でなんとなく理解しました。

ふむふむ、対数スケールのグラフ上に、見た目で一様になるように分布すればいいのね。
理解を助けるために、まず、対数の数直線を書いてみましょう。

runif関数で発生させた乱数をそのまま使っちゃだめですよね。それでは数値的な一様になってしまいますから。
数直線に指数表記を追加すると分かりやすいです。

指数の肩のところがリニアになっているわけですから、発生させた一様な乱数を指数の肩のところに入れて得られた数値をサンプルとすればよさそうです。
これの実行結果が↓これです。じゃん。
おお、前述のウィキペディアにあげてあった表の数値と全く同じ結果になりました。
最後にヒストグラムを描いてみましょう。

うん、ここまでやると納得できましたね。
数字の出方に法則性があるようにも思えないから、1から9まで一様になっているのでは? という気もしますが、そうではないというのがベンフォードの法則です。
ベンフォードの法則 - Wikipedia
ベンフォードの法則は、自然界に出てくる多くの(全てのではない)数値の最初の桁の分布が一様ではない、ある特定のものになっているというものである。
(中略)
この直感に反するような結果は、電気料金の請求書、住所の番地、株価、人口の数値、死亡率、川の長さ、物理・数学定数、冪乗則で表現されるような過程(自然界ではとても一般的なものである)など、様々な種類の数値の集合に適用できることがわかっている。
どのように偏って分布しているかというと、↓こんな割合になるとのこと。

ベンフォードの法則 - Wikipedia より
本当にそうなるか、Rでシミュレーションしてみましょう。
数値が満たすべき分布について、ウィキペディアには、
論理的には、数値が対数的に分布しているときは常に最初の桁の数値がこのような分布で出現する。
とあります。いまいちピンとこなかったのですが、あわせて掲載されていた図でなんとなく理解しました。

ふむふむ、対数スケールのグラフ上に、見た目で一様になるように分布すればいいのね。
理解を助けるために、まず、対数の数直線を書いてみましょう。

runif関数で発生させた乱数をそのまま使っちゃだめですよね。それでは数値的な一様になってしまいますから。
数直線に指数表記を追加すると分かりやすいです。

指数の肩のところがリニアになっているわけですから、発生させた一様な乱数を指数の肩のところに入れて得られた数値をサンプルとすればよさそうです。
n <- 1000000 # サンプルサイズ(これくらいだとやや時間かかる) u <- runif(n, 0, 3) # 0~3の範囲の一様乱数 x <- 10^u # 乱数の指数の肩に msd <- as.integer(substr(x, 1, 1)) # 最上位桁の取り出し round(table(msd) / n * 100, 1) # 割合をパーセントで表示
これの実行結果が↓これです。じゃん。
msd 1 2 3 4 5 6 7 8 9 30.1 17.6 12.5 9.7 7.9 6.7 5.8 5.1 4.6
おお、前述のウィキペディアにあげてあった表の数値と全く同じ結果になりました。
最後にヒストグラムを描いてみましょう。

うん、ここまでやると納得できましたね。


コメント
コメントを投稿