Rのcontour(等高線)を使って陰関数のグラフを描く

Rで、y = f(x) という形の関数のグラフを描きたければ、curve関数を使えばいいですよね。

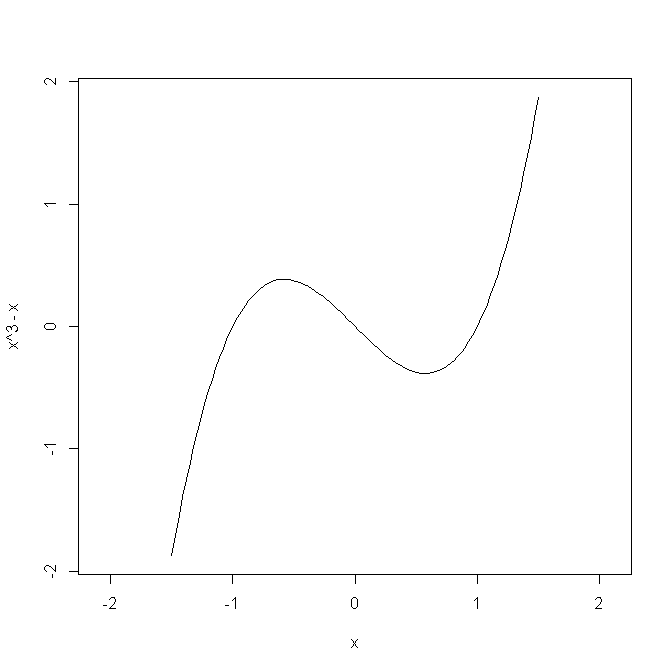curve関数で描いた3次曲線のグラフ

curve( x^3 - x, from=-1.5, to=1.5, asp=1)

で、簡単にいきそうにないのは、f(x,y) = 0 という形。陰関数ってやつですね。x^2 + y^2 = 1とかも一例ですね。この例みたいな円の方程式くらいだったら、yについて解いちゃうとか、x=cos(t),y=sin(t)みたいに媒介変数を使う方法もあるんですが、この方法が任意の陰関数について使えるというわけではない。

で、どうやるかというと、答えは↓ここにあります。

陰関数で表された曲線の描画 - 裏 RjpWiki


z = f(x,y) みたいに考えて、xy平面の各格子点に対してzの値を計算する。そして、contour関数を使って等高線を引く。その際、levels=0とオプション指定すれば、f(x,y) = 0のところに線が引かれるという、ちょっとトリッキーなやり方ですが、これで任意の陰関数のグラフが描けるので、とてもうれしいです。

この手法を理解するために、あえて簡単なサンプルをあげてみます。

contour関数で描いた円のグラフ

n <- 10 # メッシュ分割数
x <- seq( -1, 1, length = n )
y <- seq( -1, 1, length = n )
z <- matrix(0, n, n)
for (i in 1:n) {
  for (j in 1:n) {
    z[i, j] <- x[i] ^ 2 + y[j] ^ 2 # ここに陰関数を書く
  }
}
contour(x, y, z, drawlabels = F, levels=1, asp=1)

円がちょっと多角形っぽく見えるのはnが小さいからです。大きくすればなめらかな曲線になります。

この手法、contour関数を使ったことないとピンとこないですよね。

計算されたzの値を見てみると分かりやすいと思います。

> round(z,2)
      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,] 2.00 1.60 1.31 1.11 1.01 1.01 1.11 1.31 1.60  2.00
 [2,] 1.60 1.21 0.91 0.72 0.62 0.62 0.72 0.91 1.21  1.60
 [3,] 1.31 0.91 0.62 0.42 0.32 0.32 0.42 0.62 0.91  1.31
 [4,] 1.11 0.72 0.42 0.22 0.12 0.12 0.22 0.42 0.72  1.11
 [5,] 1.01 0.62 0.32 0.12 0.02 0.02 0.12 0.32 0.62  1.01
 [6,] 1.01 0.62 0.32 0.12 0.02 0.02 0.12 0.32 0.62  1.01
 [7,] 1.11 0.72 0.42 0.22 0.12 0.12 0.22 0.42 0.72  1.11
 [8,] 1.31 0.91 0.62 0.42 0.32 0.32 0.42 0.62 0.91  1.31
 [9,] 1.60 1.21 0.91 0.72 0.62 0.62 0.72 0.91 1.21  1.60
[10,] 2.00 1.60 1.31 1.11 1.01 1.01 1.11 1.31 1.60  2.00

↓xy平面上にzの値をプロットしてみました

zの値をxy平面にプロット

plot( x, y, xlim=c(-1,1), ylim=c(-1,1), type="n", asp=1)
for (i in 1:10) {
  for (j in 1:10) {
    text( (i-5.5)/4.5, (j-5.5)/4.5, sprintf("%1.2f", z[i,j]))
  }
}

上記のz値の値に対して、z = 1 のところに等高線を引くと下記のようになり、

zの値のプロットと、z = 1 の等高線(contour)

plot( x, y, xlim=c(-1,1), ylim=c(-1,1), type="n", asp=1)
for (i in 1:10) {
  for (j in 1:10) {
    text( (i-5.5)/4.5, (j-5.5)/4.5, sprintf("%1.2f", z[i,j]))
  }
}
contour(x, y, z, drawlabels = F, levels=1, add=T)

これが、この手法の仕組みとなります。

levelsオプションにベクトルで複数の値を指定すると、より等高線っぽくなります。drawlabels(線が示す値)も表示してみましょう↓

z = 0.1, 0.5, 1.0, 1.5 の等高線(contour)

contour(x, y, z, drawlabels = T, levels=c(0.1, 0.5, 1, 1.5), asp=1)

この手法の仕組み、理解していただけましたでしょうか。これで、いろんな陰関数のグラフを描きまくってください。